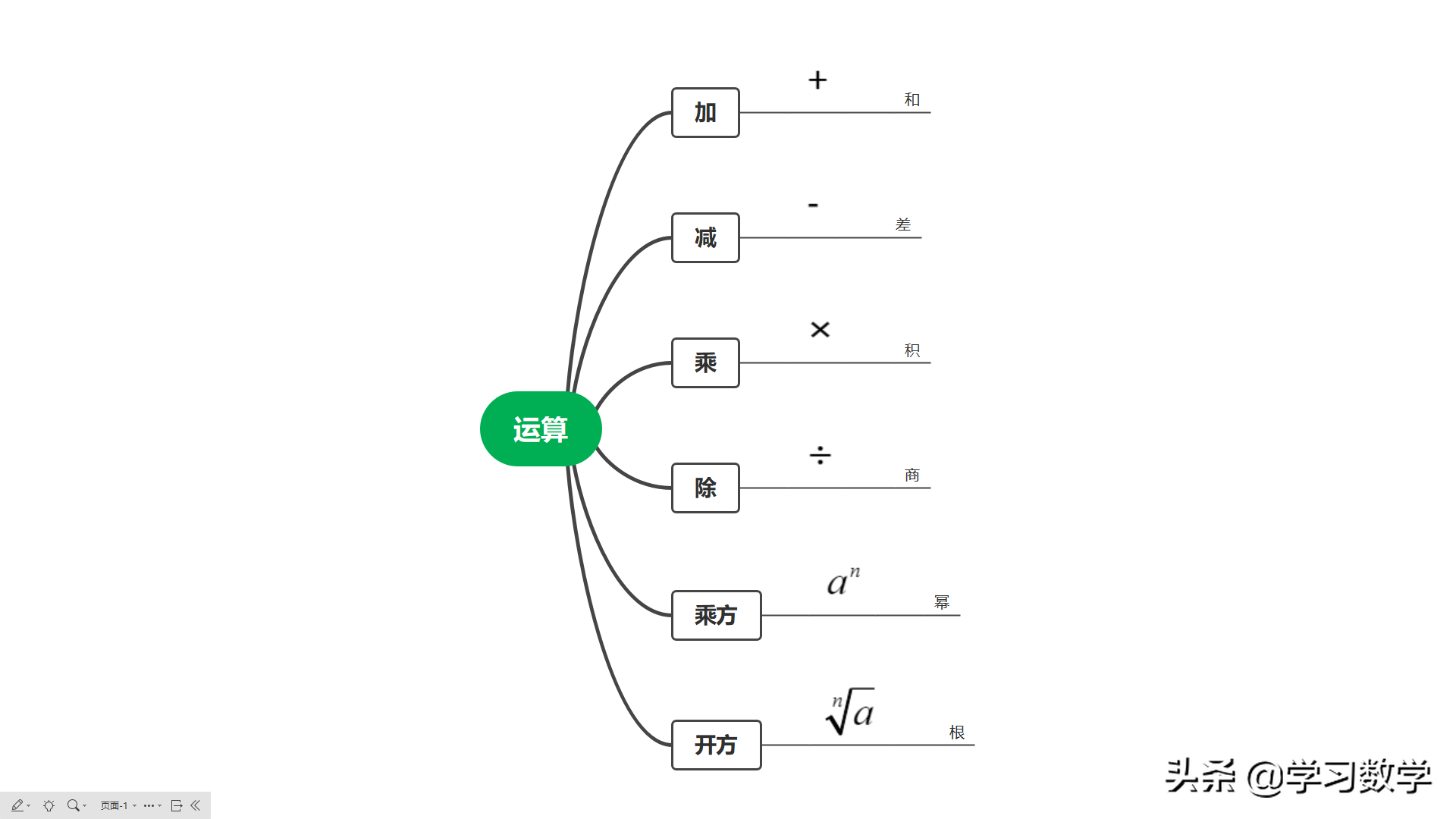
请注意立方差公式推广，新引入的平方根符号称为根号。 参考加法、减法、乘法和除法来理解。 它也是一个操作符号。

学生应该理解被数与被减数和被除数的结合，以及根指数与幂指数的结合。

我们知道幂包括2次方、3次方……n次方。 初中主要研究的是2次方和3次方，也就是常说的平方和立方。 至于互逆和对应的平方根运算，我们在初中阶段也主要学习2次方（平方根）和3次方（立方根）。 平方根的结果是平方根，立方根的结果是立方根。

理解并记住，只有非负数才有平方根，负数没有平方根。 实数a（a≥0）有两个平方根（0的平方根为0），它们互为相反数。 一个数的平方根仍然等于该数的平方。 （结合加减乘除的倒数运算的理解）

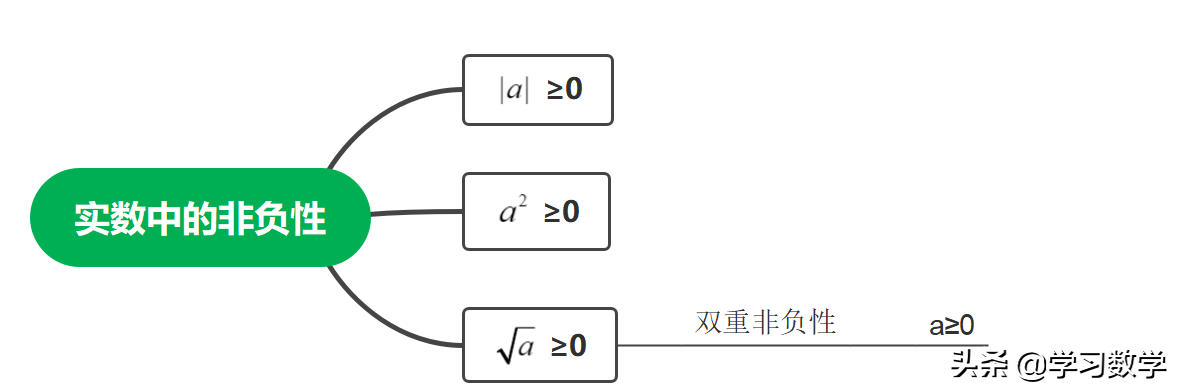
非负数a的两个平方根的正平方根称为a的算术平方根。 有必要了解算术平方根的双重非负性。

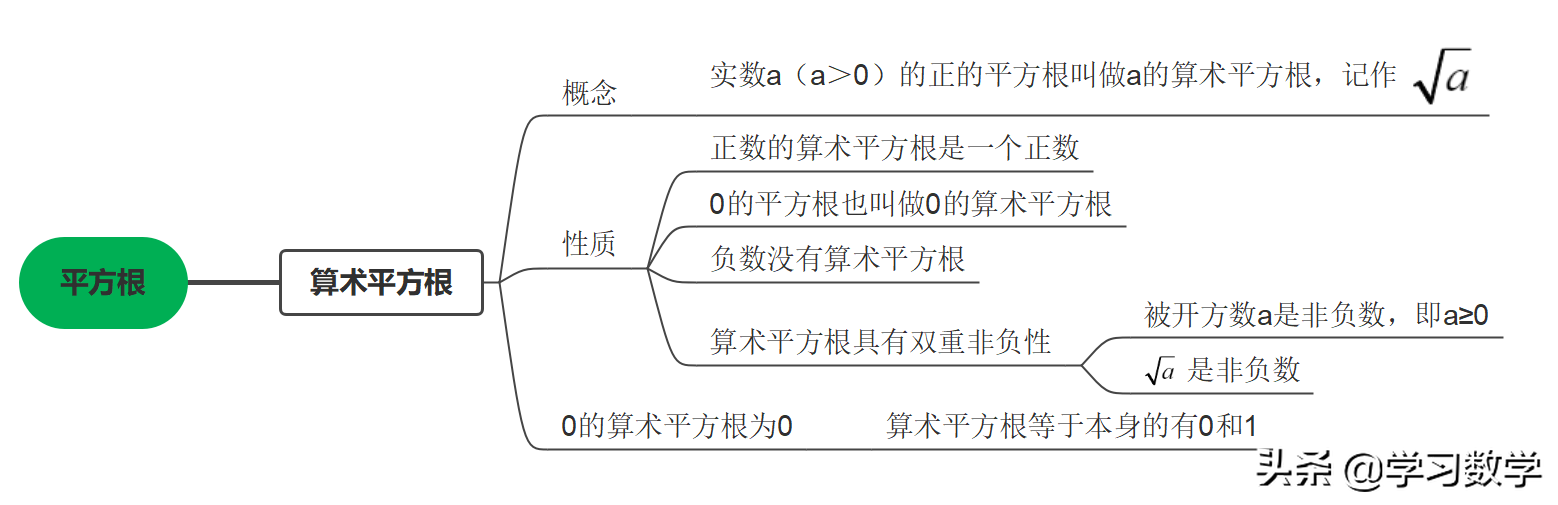
你需要知道平方根的表示立方差公式推广，熟悉基本知识点和性质，能够将绝对值与根符号结合起来。

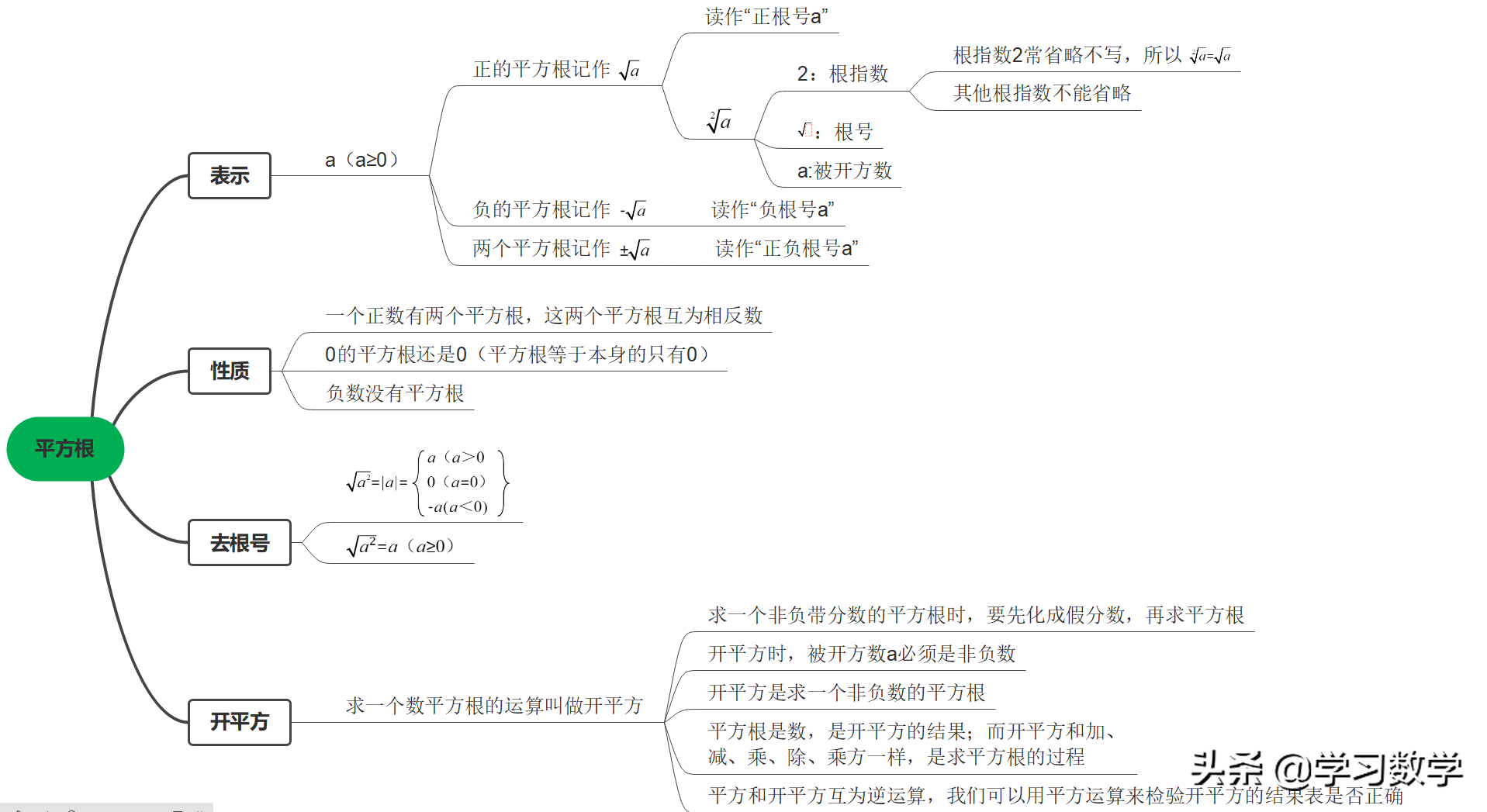
然后在掌握平方根的基础上了解立方根，并注意两者之间的联系和区别。

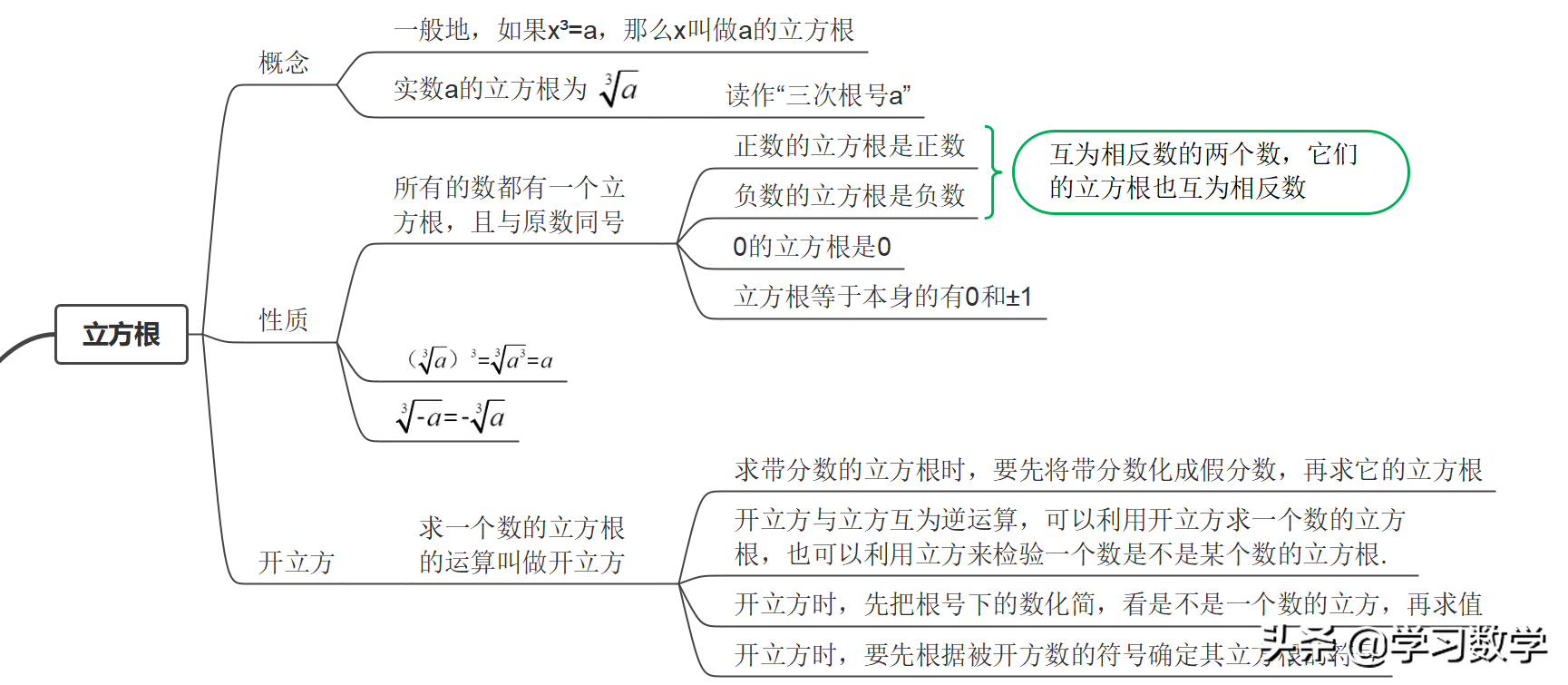
初中阶段的三类非负数必须牢固掌握并熟练运用。

例1：已知2a-1的平方根为±3，3a+2b+4的立方根为3。求a+b的平方根。

分析：首先，根据平方根和立方根的定义，得到关于a和b的二变量线性方程组。 然后我们就可以求解方程组。

求出a和b的值，然后得到a+b的平方根。

例2：已知m+n和m_n分别是9的两个平方根，m+n_p的立方根为1，求n+p的值

分析：①一个数有两个平方根，且互为相反数； ② 两个互为相反数的和是0。 ③9 的平方根是±3； ④1的立方根为1。

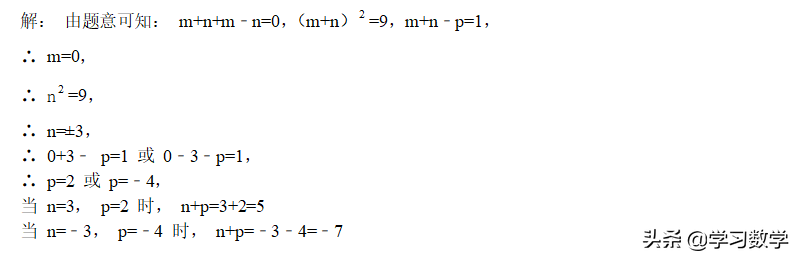
示例3：

分析：根据算术平方根的绝对值和非负性，可得x+2=0，y-3=0。 因此我们得到x=-2，y=3。 所以x+y=1，最终答案是1。

本站对作者上传的所有内容将尽可能审核来源及出处，但对内容不作任何保证或承诺。请读者仅作参考并自行核实其真实性及合法性。如您发现图文视频内容来源标注有误或侵犯了您的权益请告知，本站将及时予以修改或删除。